Euclides de Alexandria (360 a.C. — 295 a.C.)
um professor, matemático platónico e escritor possivelmente grego, muitas vezes referido como o "Pai da Geometria". Ele era ativo em Alexandria durante o reinado de Ptolomeu I(323-283 a.C.). Sua obra Os Elementos é uma das mais influentes na história da matemática, servindo como o principal livro para o ensino de matemática (especialmente geometria) desde a data da sua publicação até o fim do século XIX ou início do século XX. Nessa obra, os princípios do que é hoje chamado de geometria euclidiana foram deduzidos a partir de um pequeno conjunto de axiomas. Euclides também escreveu obras sobre perspectivas, seções cônicas, geometria esférica, teoria dos números e rigor.
A geometria euclidiana é caracterizada pelo espaço euclidiano, imutável, simétrico e geométrico, metáfora do saber na antiguidade clássica e que se manteve incólume no pensamento matemático medieval e renascentista, pois somente nos tempos modernos puderam ser construídos modelos de geometrias não-euclidianas.
 Euclides.
Euclides.Vida
Pouco se sabe sobre a vida de Euclides, pois há apenas poucas referências a ele. Na verdade, as referências fundamentais sobre Euclides foram escritas séculos depois que ele viveu, por Proclo e Pappus de Alexandria. Proclo apresenta Euclides apenas brevemente no seu Comentário sobre os Elementos, escrito no século V, onde escreve que Euclides foi o autor de Os Elementos, que foi mencionado por Arquimedes e que, quando Ptolomeu I perguntou a Euclides se não havia caminho mais curto para a geometria que Os Elementos, ele respondeu: "não há estrada real para a geometria". Embora a suposta citação de Euclides por Arquimedes foi considerada uma interpolação por editores posteriores de suas obras, ainda se acredita que Euclides escreveu suas obras antes das de Arquimedes. Além disso, a anedota sobre a "estrada real" é questionável, uma vez que é semelhante a uma história contada sobre Menecmo e Alexandre, o Grande. Na outra única referência fundamental sobre Euclides, Pappus mencionou brevemente no século IV que Apolônio "passou muito tempo com os alunos de Euclides em Alexandria, e foi assim que ele adquiriu um hábito de pensamento tão científico". Também se acredita que Euclides pode ter estudado na Academia de Platão, na Grécia.
A data e local de nascimento de Euclides e da data e as circunstâncias de sua morte são desconhecidas, e só aproximadamente estimada pela comparação com as figuras contemporâneas mencionadas nas referências. Nenhuma imagem ou descrição da aparência física de Euclides foi feita durante sua vida, em que foi vivida na antiguidade. Portanto, representação de Euclides em obras de arte é o produto da imaginação do artista.
Convidado por Ptolomeu I para compor o quadro de professores da recém fundada Academia, que tornaria Alexandria o centro do saber da época, tornou-se o mais importante autor de matemática da Antiguidade greco-romana e talvez de todos os tempos, com seu monumentalStoichia (Os elementos, 300 a.C.), no estilo livro de texto, uma obra em treze volumes, sendo cinco sobre geometria plana, três sobre números, um sobre a teoria das proporções, um sobre incomensuráveis e os três últimos sobre geometria no espaço. Escrita em grego, a obra cobria toda a aritmética, a álgebra e a geometria conhecidas até então no mundo grego, reunindo o trabalho de seus predecessores, como Hipócrates e Eudóxio, e sistematizava todo o conhecimento geométrico dos antigos e intercalava os teoremas já conhecidos então com a demonstração de muitos outros, que completavam lacunas e davam coerência e encadeamento lógico ao sistema por ele criado. Após sua primeira edição foi copiado e recopiado inúmeras vezes e, vertido para o árabe (774), tornou-se o mais influente texto científico de todos os tempos e um dos com maior número de publicações ao longo da história. Depois da queda do Império Romano, os seus livros foram recuperados para a sociedade européia pelos estudiosos muçulmanos da península Ibérica. Escreveu ainda Óptica (295 a.C.), sobre a óptica da visão e sobre astrologia, astronomia, música e mecânica, além de outros livros sobre matemática. Entre eles citam-se Lugares de superfície, Pseudaria, Porismas e mais algumas outras.
Algumas das suas obras como Os elementos, Os dados, outro livro de texto, uma espécie de manual de tabelas de uso interno na Academia e complemento dos seis primeiros volumes de Os Elementos, Divisão de figuras, sobre a divisão geométrica de figuras planas,Os Fenômenos, sobre astronomia, e Óptica, sobre a visão, sobreviveram parcialmente e hoje são, depois de A Esfera de Autólico, os mais antigos tratados científicos gregos existentes. Pela sua maneira de expor nos escritos deduz-se que tenha sido um habilíssimo professor.
Os Elementos
Embora muitos dos resultados em Os Elementos tiveram origem em matemáticos anteriores, uma das habilidades de Euclides foi apresentá-los em uma única estrutura logicamente coerente, tornando-a fácil de usar e de fácil referência, incluindo um sistema rigoroso de provas matemáticas que continua a ser a base da matemática 23 séculos mais tarde.
Não há menção de Euclides nas primeiras cópias ainda remanescentes de Os Elementos, e a maioria das cópias dizem que são "a partir da edição de Theon" ou as "palestras de Theon", enquanto o texto considerado primário, guardado pelo Vaticano, não menciona qualquer autor. A única referência que os historiadores se baseiam para Euclides ter escritoOs Elementos veio de Proclo, que brevemente em seu Comentário sobre Os Elementosatribui Euclides como o seu autor.

Euclides

Um dos mais antigos fragmentos sobreviventes de Os Elementos de Euclides, encontrado entre os Papiros de Oxirrinco e datado de cerca de 100 d.C. O diagrama acompanha o Livro II, Proposição 5.
Curiosidades.
Euclides é a versão aportuguesada da palavra grega Εὐκλείδης, que significa "Boa Glória".
Algoritmo de Euclides
Em matemática, o algoritmo de Euclides é um método simples e eficiente de encontrar o máximo divisor comum entre dois números inteiros diferentes de zero. É um dos algoritmos mais antigos, conhecido desde que surgiu nos Livros VII e X da obra Elementos de Euclides por volta de 300 a.C.. O algoritmo não exige qualquer fatoração.
O MDC de dois números inteiros é o maior número inteiro que divide ambos sem deixar resto. O algoritmo de Euclides é baseado no princípio de que o MDC não muda se o menor número for subtraído ao maior. Por exemplo, 21 é o MDC de 252 e 105 (252 = 21 × 12; 105 = 21 × 5); já que 252 − 105 = 147, o MDC de 147 e 105 é também 21. Como o maior dos dois números é reduzido, a repetição deste processo irá gerar sucessivamente números menores, até convergir em zero. Nesse momento, o MDC é o outro número inteiro, maior que zero. Ao reverter os passos do algoritmo de Euclides, o MDC pode ser expresso como soma dos dois números originais, cada um multiplicado por um número inteiro positivo ou negativo, por exemplo, 21 = 5 × 105 + (−2) × 252. Esta importante propriedade é denominada identidade de Bézout.
A mais antiga descrição que se conhece do método usado no algoritmo de Euclides é da sua obraElementos (c. 300 a.C.), o que o torna um dos algoritmos numéricos mais antigos ainda em uso corrente. O algoritmo original foi descrito apenas para números naturais e comprimentos geométricos, mas foi generalizado no século XIX para outras classes de números como os inteiros gaussianos e polinómios de uma variável. Isto conduziu a noções da moderna álgebra abstrata tais como os domínios euclidianos. O algoritmo de Euclides foi ainda generalizado mais a outras estruturas matemáticas, como os nós e polinómios multivariados.

Animação do algoritmo de Euclides para os inteiros 252 e 105. As barras representam múltiplos de 21, o máximo divisor comum (MDC). Em cada passo, o número menor é subtraído ao maior, até um número ser reduzido a zero. O número restante é o MDC.
História do desenvolvimento do algoritmo
O algoritmo de Euclides é um dos mais antigos algoritmos ainda em uso. Surge na sua obra Os Elementos (c. 300 a.C.), especificamente nos Livros 7 (Proposições 1–2) e 10 (Proposições 2–3). No Livro 7, o algoritmo é formulado para inteiros, enquanto no Livro 10 é formulado para comprimentos de segmentos lineares (dir-se-ia hoje que estaria formulado para números reais. Comprimentos, áreas e volumes, representados como números reais hoje em dia, não são medidos nas mesmas unidades, e não existe uma unidade natural de comprimento, área ou volume. O conceito de número real era desconhecido à época de Euclides. O último algoritmo é geométrico. O MDC de dois comprimentosa e b corresponde ao maior comprimento g que mede propriamente a e b; por outras palavras, os comprimentos a e b são o resultado da multiplicação do comprimento g por números inteiros.
O algoritmo não foi provavelmente concebido por Euclides, que compilou resultados de matemáticos anteriores nos seus Elementos. O matemático e historiador Bartel van der Waerden sugere que o Livro VII provém de um texto em teoria dos números escrito por matemáticos da escola de Pitágoras. O algoritmo era provavelmente conhecido por Eudoxo de Cnido (cerca de 375 a.C.). Poderá ainda ser anterior a Eudoxo, a julgar pelo uso do termo técnico ἀνθυφαίρεσις (anthyphairesis, subtração recíproca) em trabalhos de Euclides e Aristóteles.
Séculos mais tarde, o algoritmo de Euclides terá sido reinventado de forma independente na Índia e China sobretudo para resolver equações diofantinas que surgiram relacionadas com a Astronomia e a elaboração de calendários precisos. No final do século V, o matemático indiano e astrónomo Aryabhata descrevu o algoritmo como o "pulverizador", por causa da sua eficácia a resolver equações diofantinas. Embora um caso especial do teorema chinês do resto já fora descrito pelo matemático e astrónomo chinês Sun Tzu, a solução geral foi publicada por Ch’in Chiu-Shao na sua obra de 1247 chamada Shushu Jiuzhang (數書九章 Tratado Matemático em Nove Partes). O algoritmo de Euclides foi descrito pela primeira vez na Europa na segunda edição de Problèmes plaisants et délectables (Problemas aprazíveis e deleitáveis, 1624) de Bachet de Méziriac .Na Europa, era usado para resolver equações diofantinas e desenvolvimento de frações contínuas. O algoritmo de Euclides estendido foi publicado pelo matemático inglês Nicholas Saunderson, que o atribuiu a Roger Cotes como método para calcular frações contínuas de forma eficiente.
Descrição do algoritmo
Na concepção grega da matemática, os números eram entendidos como magnitudes geométricas. Um tema recorrente na geometria grega era o da comensurabilidade de dois segmentos: dois segmentos (números) AB e CD são comensuráveis quando existe um terceiro segmento PQ que cabe exactamente um número inteiro de vezes nos primeiros dois, ou seja, PQ «mede» (mensura: medida) os segmentos AB e CD.
Nem todos os pares de segmentos são comensuráveis, como observaram os pitagóricos quando estabeleceram que  não é um número racional, mas no caso de dois segmentos comensuráveis pretende-se determinar a maior medida comum possível.
não é um número racional, mas no caso de dois segmentos comensuráveis pretende-se determinar a maior medida comum possível.
 não é um número racional, mas no caso de dois segmentos comensuráveis pretende-se determinar a maior medida comum possível.
não é um número racional, mas no caso de dois segmentos comensuráveis pretende-se determinar a maior medida comum possível.Euclides descreveu na proposição VII.2 dos seus Elementos um método que permite determinar a maior medida comum de dois números (segmentos) que não sejam primos entre si, embora na época tal método se explicasse em termos geométricos, o que se ilustra na transcrição seguinte:
Sejam AB e CD os dois números que não são primos entre si. É necessário então encontrar a máxima medida comum de AB e CD.Se CD mede AB então é uma medida comum já que CD se mede a si mesmo. É manifesto que também é a maior medida pois nada maior que CD pode medir CD. Mas se CD não mede AB então algum número restará de AB e CD, o menor sendo continuamente resto do maior e que medirá o número que o precede. Porque uma unidade não ficará pois se assim não for, AB e CD serão primos entre si [Prop. VII.1], o que é contrário ao que se supôs.Portanto, ficará algum número que medirá o número que o precede. E seja CD a medir BE deixando EA menor que si mesmo e seja EAmedindo DF deixando FC menor que si mesmo e seja FC medida deAE. Então, como FC mede AE e AE mede DF, FC será então medida de DF. E também se mede a si mesmo. Portanto também medirá todo o segmento CD. e CD mede BE. Então CF mede BE e também medeEA. Assim mede todo o segmento BA e também mede CD. Isto é, CFmede tanto AB como CD, pelo que é uma medida comum de AB e CD.Afirmo que também é a maior medida comum possível porque se não o fosse, então um número maior que CF mede os números AB e CD. Seja este G. Dado que G mede CD e CD mede BE, G também medeBE. Além disso, mede todo o segmento BA pelo que mede também o resíduo AE. E AE mede DF pelo que G também mede DF. Mede ainda todo o segmento DC pelo que mede também o resíduo CF, ou seja, o maior mede o menor, o que é impossível.Portanto, nenhum número maior que CF pode medir os números AB eCD. Então CF é a maior medida comum de AB e CD, o que era o que se queria demonstrar.—Euclides. Elementos VII.2
Demonstração da terminação e exatidão do algoritmo
A própria definição da série (an) por divisão euclidiana mostra que, para qualquer n tal que an + 1 é não nulo, existe um inteiro qn + 2tal que : 

e ainda  . A série de inteiros naturais (an) é portanto estritamente decrescente, e atingirá o valor 0 num número finito de passos. A existência de um último resto não nulo está assim estabelecida.
. A série de inteiros naturais (an) é portanto estritamente decrescente, e atingirá o valor 0 num número finito de passos. A existência de um último resto não nulo está assim estabelecida.
 . A série de inteiros naturais (an) é portanto estritamente decrescente, e atingirá o valor 0 num número finito de passos. A existência de um último resto não nulo está assim estabelecida.
. A série de inteiros naturais (an) é portanto estritamente decrescente, e atingirá o valor 0 num número finito de passos. A existência de um último resto não nulo está assim estabelecida.Seja N + 1 o índice deste último resto não nulo. Para mostrarar que aN + 1 é o MDC procurado, note-se que a relação anterior se escreve como 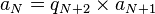 , o que mostra que aN + 1 divide aN. Tomando
, o que mostra que aN + 1 divide aN. Tomando  , deduz-se que aN + 1 divide também aN − 1 ; também, e por recorrência, note-se que aN + 1 divide todos os termos da série an ; em particular os primeiros termos a e b. aN + 1 é então um divisor comum de a e b. Reciprocamente, todo o divisor comum de a e b dividirá também
, deduz-se que aN + 1 divide também aN − 1 ; também, e por recorrência, note-se que aN + 1 divide todos os termos da série an ; em particular os primeiros termos a e b. aN + 1 é então um divisor comum de a e b. Reciprocamente, todo o divisor comum de a e b dividirá também 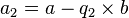 , e de novo por recorrência, dividirá todos os termos da série (an) ; em particular aN + 1.
, e de novo por recorrência, dividirá todos os termos da série (an) ; em particular aN + 1.
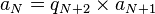 , o que mostra que aN + 1 divide aN. Tomando
, o que mostra que aN + 1 divide aN. Tomando  , deduz-se que aN + 1 divide também aN − 1 ; também, e por recorrência, note-se que aN + 1 divide todos os termos da série an ; em particular os primeiros termos a e b. aN + 1 é então um divisor comum de a e b. Reciprocamente, todo o divisor comum de a e b dividirá também
, deduz-se que aN + 1 divide também aN − 1 ; também, e por recorrência, note-se que aN + 1 divide todos os termos da série an ; em particular os primeiros termos a e b. aN + 1 é então um divisor comum de a e b. Reciprocamente, todo o divisor comum de a e b dividirá também 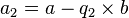 , e de novo por recorrência, dividirá todos os termos da série (an) ; em particular aN + 1.
, e de novo por recorrência, dividirá todos os termos da série (an) ; em particular aN + 1.aN + 1 é então um divisor comum de a e b que é divisível por todo e qualquer divisor comum: é assim o MDC.



Nenhum comentário:
Postar um comentário